Introduction
Proudly running the ERATO MMSD project. Visit its introduction.
(Old Version, as of 2014?)
(Old Version, as of 2012) Mathematical Structures in Computing and Computer Systems
My research activities aim at pushing forward the use of abstract mathematics (esp. the language of category theory) in computer science (esp. system/program verification), where mathematical logic also plays an important role. Specific topics include:
-
An algebraic/coalgebraic approach to concurrency theory, including
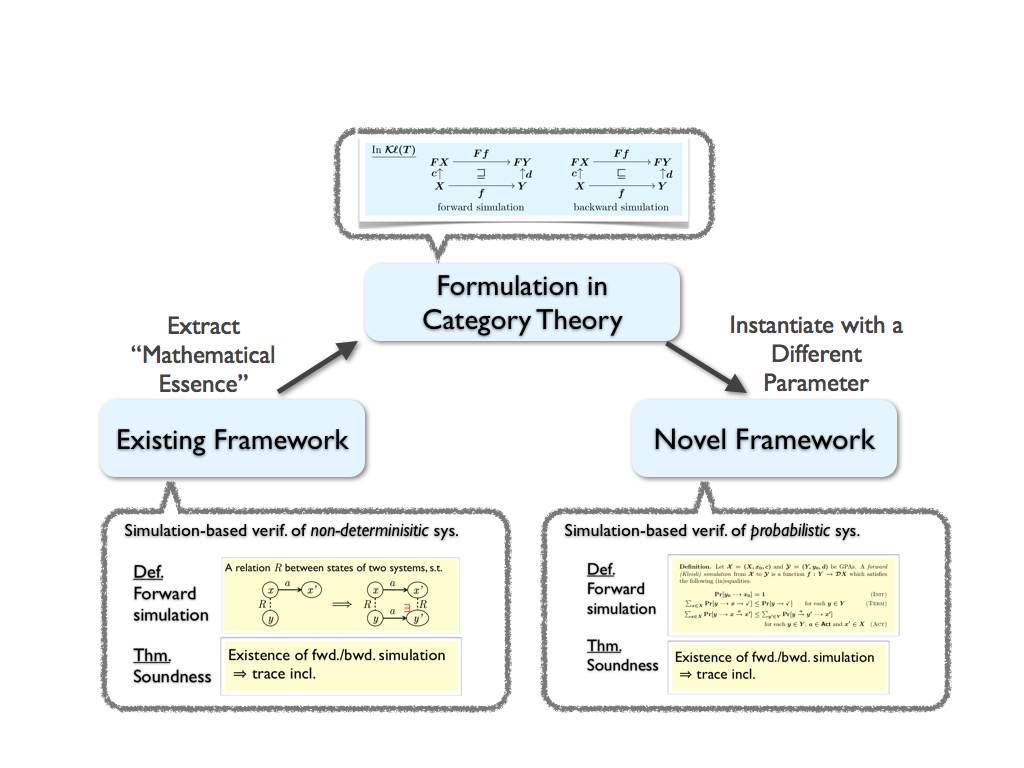
- General theory of trace semantics and simulations via coalgebras in a Kleisli category [Hasuo-Jacobs-Sokolova LMCS'07][Hasuo CONCUR'06][Hasuo CONCUR'10]
- Its application in verification of systems and network protocols [Hasuo-Kawabe-Sakurada TCS'10]
- The microcosm principle–a mathematical structure that arises in component-based design of systems–and its implications in software engineering [Hasuo-Jacobs-Sokolova FoSSaCS'08][Asada-Hasuo CMCS'10][Hasuo-Jacobs MSCS'10]
- Quantum programming languages. We aim to transfer–exploiting the genericity of the categorical language–the rich theory of (classical) programming languages to quantum settings [Hasuo-Hoshino '11]
- Information Security: logical formalization of information security properties and their verification techniques [Garcia-Hasuo-Pieters-van Rossum FMSE'05][Hasuo-Jacobs JCS'09][Hasuo-Kawabe-Sakurada TCS'10]
I believe in the advantages of our mathematical approach:
- We can sometimes transfer an existing technique to a new application domain, via its mathematical (abstract) formulation (see Figure). This "lifting" methodology works particularly well for new computing paradigms like quantum or hybrid.
- A resulting theory sometimes comes with unexpected generality; its application domain can go beyond computer science (we have such an experience for fractals [Hasuo-Jacobs-Niqui MFPS'10])